
The red-brick building seen on the right of the photograph is the riverside building (ca. 1460), the oldest building on the river at Cambridge, containing parts of the President’s Lodge.
For old views and prints of this bridge, see: Bridges and Riverside.
Quick briefing
- The design is a minor triumph of mid-18th century engineering, for which credit must go to James King (d. 1744);
- The bridge spans a 50-foot river using multiple shorter lengths of timber: for instance, the horizontal element which appears to span the entire river is made of six shorter timbers jointed end-to-end;
- The design is an implementation in timber of a voussoir arch bridge, in which the individual elements are held in a state of compression by the action of gravity on the whole structure: a voussoir bridge requires strong abutments to balance the compressive forces at the springing of the arch;
- Wood is a weak material if subjected to bending (consider how easy it is to break a match by bending it): in this bridge design, the timbers in the side trusses are subjected to little or no bending forces: the dominant force in the timbers tangential to the arch is simple compression, in which state wood is very strong (consider how difficult it is to break a match by pressing its ends together without bending it);
- The triangulation in the side trusses makes them stiff, without being too heavy, and prevents hinging at the joints between segments of the arch;
- The lack of in-fill of the sides reduces the impact of side-winds on the structure: the only cross-bracing is under the footway;
- It was claimed for this design that, if it were needed to replace a timber in a side truss, then that timber could be removed and replaced without disturbing its neighbours, and without needing to dismantle the entire bridge. This has never been tested in practice.
History of the Bridge at Queens’
The erection of the bridge occurred at the same time as the building of brick walls along the river banks and alterations in the layout of the Grove. It can therefore be difficult in reading the college records to distinguish one project from another. The following entries in the Magnum Journale appear to be relevant to the Bridge or riverside works:
| £. | s. | d. | ||
|---|---|---|---|---|
| 1748 Oct 6 | Mr Etheridge for the Design & Model of the Bridge | 21. | 00. | 00 |
| 1749 Mar 25 | Paid for removeing the Mud from the Bridge | 01. | 02. | 6 |
| 1749 Jul 1 | Paid for five Men for digging the River Bank | 01. | 11. | 6 |
| 1749 Jul 8 | Paid for six Men for digging the River Bank | 02. | 01. | 6 |
| 1749 Sep 30 | Paid for work in levelling the River Bank | 0. | 07. | 6 |
| „ | Two Men levelling the Bank at the Bridge | 0. | 07. | 0 |
| „ | 300 Green Turf for the River Bank | 0. | 18. | 0 |
| „ | Paid Wm Christmas for the Use of a Boat | 00. | 03. | 0 |
| „ | Mr Groom for the Use of a Boat | 03. | 00. | 0 |
| „ | Mr Tucke, the Bricklayer’s Bill | 114. | 16. | 8 |
| „ | Mr Bottomley, the Mason’s Bill | 151. | 12. | 9 |
| „ | Mr Essex’s Bill for the new Bridge | 160. | 00. | 0 |
| 1750 Sep 30 | Cook ... a Supper on finishing the Bridge to Mr Essex’s Men | 0. | 17. | 9 |
It was the practice to account for the bills of tradesmen (including the College’s own cook) in a single lump sum on the last day of the academic year, so nothing much can be deduced about the timing of works accounted for on September 30th, other than that they were paid for sometime in the previous twelve months. The supper that was accounted for in September 1750 might have occurred as early as October 1749. As Essex was paid in the year ending September 1749, it is reasonable to assume that all the works were executed during the summer of 1749. Willis & Clark appear to have been in error in stating that the bridge was finished in September, 1750
. [The Architectural History of the University of Cambridge by Willis & Clark, Vol. 2, p. 56]
 The college possesses an old model of the bridge, and we assume that this is Etheridge’s model of 1748 (although we have no proof of this). The model is at 1⁄16th scale.
The college possesses an old model of the bridge, and we assume that this is Etheridge’s model of 1748 (although we have no proof of this). The model is at 1⁄16th scale.
Things to be noted about this model are: (a) it has screw-eyes at all the joints in the truss, including the lap joints of the tangential members; and (b) the pedestrian decking is stepped, rather than sloped, just as the real bridge was stepped until the repairs of 1866.
The earliest printed description of the bridge appeared in 1753:
The Bridge from the Cloister to the Stable, &c. which was wholly rebuilt A.D. 1746; may without Flattery, be esteemed one of the most curious pieces of Carpentery of this kind in England, it contains in length upwards of 50 Foot, being of one Arch, composed of Timbers curiously joined together, and supported on Abutments of Rustic Stone-work, between which is a Passage for the Cam, 40 Foot in the Clear, and of such Heigth[sic], that the Waters in a common Flood, cannot reach the lowest Timbers thereof.
[The History of the University of Cambridge by Edmund Carter, 1753, p. 186]
Carter was not renowned for his accuracy: the incorrect date of 1746 was reproduced in many subsequent histories and guides.
The earliest discovered use of the term Mathematical Bridge
in relation to the bridge at Queens’ was in A Guide through the University of Cambridge, of 1803, as a footnote to a description of the bridge on page 68: Usually known by the name of the Mathematical Bridge.
A different publication, Cantabrigia Depicta, by Harraden & Sons, made a similar comment in 1809. Some care is required in interpretation, as the phrase Mathematical Bridge
was also being used in the same period to describe the similar bridge at Garret Hostel Lane (see below), and either bridge might have been confused with the other.
The bridge is 50 feet 8 inches (15·44 metres) long. The angle between two adjacent radials (except the ones on the abutments) is one 32nd of a revolution. The arch is composed of tangents to a circle of radius 32 feet. [Queens’ Bridge, by Gunnar de Vries, 1992, p. 8]
The design of the Queens’ bridge resembles Etheridge’s much greater Old Walton Bridge, a three-arch bridge over the Thames, built 1748–50 (see below).
William Etheridge was one of a very long family line of carpenters called variously Edrich, Edriche, Eteridge, or Etheridge from Stradbroke and Fressingfield in Suffolk. His birth is not recorded, but his baptism took place on 3rd January 1708/09 at St Margaret’s parish church, South Elmham, about 5 miles north-east of Fressingfield. His career as a master carpenter first comes to light in 1738–49 when he worked under James King in the building of the first bridge to cross the Thames at Westminster, first as King’s foreman, then replacing him after King’s death in 1744. He was credited as the inventor of a battering ram to assist in the striking of the centres, and an underwater saw to cut off piles underwater. From 1747–50 he worked on the Walton Bridge, and in 1748 produced the design and model for the Queens’ bridge. From 1751–56 he worked as surveyor for the construction of Ramsgate Harbour in Kent. In 1761 he was consulted on the state of St Olave’s bridge at Herringfleet, Suffolk. He died aged 67 on 3rd October 1776 in Westminster and was buried on 15th October 1776 at Fressingfield. [Information in this paragraph is derived mainly from Etheridge’s family descendants, private communication].
The Queens’ Bridge is the earliest recorded built work of James Essex the Younger. He later constructed the Essex Building 1756–60, which was intended to be part of a new building along the complete riverfront, replacing the 1460s part of the President’s Lodge, but which was never completed. He is buried in St Botolph’s, church of the parish in which Queens’ lies. His father James Essex had also been a carpenter, doing work in many colleges, including the panelling of the Hall at Queens’.
Decay of, and repairs to, the Queens’ bridge
It was inevitable that any structure of wood would require occasional repair and maintenance:
Agreed that the Essex Bridge be repaired.
[Conclusion Book, 1794 Jan 17]
By the mid-19th century, the original bridge of 1749 was developing problems from the decay of certain timber elements. Judging by the photographic evidence, the main problems were the cross-beams under the bridge which connected together the lower ends of opposing radials from each side truss, and on which the load of the pedestrian decking was carried out to the side trusses. These cross-beams were horizontal, and presumably prone to water not draining away effectively, or draining into the joints with the radials of the side trusses. There was no redundancy: if a cross-beam failed, the decking would sag. We can track the development of these problems from old photographs.
 The first is a detail from a very early photograph of the bridge, and possibly the earliest surviving photograph of any Cambridge scene, taken by Thomas Craddock in the early 1850s while he was an undergraduate at Queens’ 1850–56. One of the cross-beams is shown to have been reinforced with an extra layer of timber underneath. Note that, in this period, the pedestrian decking was stepped (just like the model), rather than sloping. Those interested in demolishing myths should note that there are clearly visible fastenings at the joints of the radials and tangents on the outer side facing the camera, but that those fastenings are not visible on the inside elevation of the far side trusses.
The first is a detail from a very early photograph of the bridge, and possibly the earliest surviving photograph of any Cambridge scene, taken by Thomas Craddock in the early 1850s while he was an undergraduate at Queens’ 1850–56. One of the cross-beams is shown to have been reinforced with an extra layer of timber underneath. Note that, in this period, the pedestrian decking was stepped (just like the model), rather than sloping. Those interested in demolishing myths should note that there are clearly visible fastenings at the joints of the radials and tangents on the outer side facing the camera, but that those fastenings are not visible on the inside elevation of the far side trusses.
 We have confirmation in the next photograph, probably taken by Robert Cade, around 1857. The same cross-beam is shown with the same additional layer.
We have confirmation in the next photograph, probably taken by Robert Cade, around 1857. The same cross-beam is shown with the same additional layer.
 By the time of this next photograph (one half of a stereoscopic pair from the early to mid-1860s), the problems with the cross-beams had spread to two others, and the side trusses appear to be distorted and leaning inwards. The bridge has metal hoops strapped to pairs of radials: it is not clear whether those hoops are intended to support a canopy, or whether they are an emergency fix to prop up the side trusses.
By the time of this next photograph (one half of a stereoscopic pair from the early to mid-1860s), the problems with the cross-beams had spread to two others, and the side trusses appear to be distorted and leaning inwards. The bridge has metal hoops strapped to pairs of radials: it is not clear whether those hoops are intended to support a canopy, or whether they are an emergency fix to prop up the side trusses.
The bridge was repaired in 1866:
Agreed that the Bills for repairing the Bridge over the Cam, amounting to £348-7 having been received, that £148-7 be deducted from revenue for this year and £100 from revenue for each of the two next succeeding years.
[Conclusion Book, 1867 January 10th]
 In this photograph, ascribed to the 1870s, and definitely after the 1866 repairs, we can see that the cross-beams under the bridge have returned to their normal size and shape, with no extra layers strapped underneath. This photograph has sufficient detail to show that the side trusses appear to be unchanged: nothing appears to be new: the 1866 repairs appear to have been confined to the cross-beams under the bridge, and to the decking, which changed to be sloped rather than stepped, making it possible today for wheeled trolleys to be used over the bridge. Another change was the addition of metal clips on the top rail, to enable metal hoops to be slotted in when required. It can be seen that various timbers in the bridge have lead capping, especially near joints: presumably to keep rainwater out of the joints.
In this photograph, ascribed to the 1870s, and definitely after the 1866 repairs, we can see that the cross-beams under the bridge have returned to their normal size and shape, with no extra layers strapped underneath. This photograph has sufficient detail to show that the side trusses appear to be unchanged: nothing appears to be new: the 1866 repairs appear to have been confined to the cross-beams under the bridge, and to the decking, which changed to be sloped rather than stepped, making it possible today for wheeled trolleys to be used over the bridge. Another change was the addition of metal clips on the top rail, to enable metal hoops to be slotted in when required. It can be seen that various timbers in the bridge have lead capping, especially near joints: presumably to keep rainwater out of the joints.
 In 1905 [The Crown, 1907 Nov 2, p. 220], the bridge was completely rebuilt to the same design, by the local builder William Sindall, in teak instead of oak. Once again, the cost of the new bridge was partly buried in the costs of a larger project of works to the riverside buildings, overseen by architect Thackeray H. Turner (1853–1937), of Balfour & Turner:
In 1905 [The Crown, 1907 Nov 2, p. 220], the bridge was completely rebuilt to the same design, by the local builder William Sindall, in teak instead of oak. Once again, the cost of the new bridge was partly buried in the costs of a larger project of works to the riverside buildings, overseen by architect Thackeray H. Turner (1853–1937), of Balfour & Turner:
Agreed that the Junior Bursar should arrange with Mr Thackeray Turner about the work to be done on the River Side of the Lodge.
[Conclusion Book, 1903 April 24]
The only payment attributable solely to the new bridge was the final one of £207 6s 6d, dated 1905 September 30 in the account books (meaning that the amount had been paid to the contractor at some point in the previous 12 months). In this version of the bridge, the joints were fastened by coach-bolts passing right through each joint, the nuts being on the outer elevations, and the bolt heads being on the internal elevations of the side trusses, and therefore visible to people passing over the bridge. In the pre-1905 bridge, the fastenings at the joints had not been visible on the inside elevation of the side trusses: this might have been either (a) because the fastenings had been coach-screws driven in from the outer elevation, not penetrating to the inside elevation, or (b) because the fastening had been rebated on the inside elevation and covered with a wood shim. In the 1905 bridge, fastenings are visible at the cross-over between tangents (intermediate between radials), where no fastenings had been visible before 1905. One may speculate that perhaps the sight of bolt heads where none had been seen before might have given rise to the myth of the failed re-assembly. This myth has not been found in print earlier than the 20th century.
Principles of the design
As exhibited in the Queens’ version of the design, the main members of each truss are set at tangents to the circle describing the underside of the arch of the bridge. In the bottom arch itself, each tangential member is in compression with little or no bending moment, an ideal application of wood as a structural material. Where the tangential members cross each other in the arch, the wood joint (a form of lap splice joint) transmits the compressive stress from one tangent member to the next, with a bolt serving to hold the joint together laterally, rather than itself carrying any stress. The tangential members, although appearing long, are in fact composed of multiple shorter lengths of timber, joined with tabled splice joints: the ends of each lap are concealed either (a) inside the joint with a radial member, or (b) at a cross-over with another tangential member. The radial members both (a) support the top rail, and (b) lock all the overlapping tangents into a rigid truss, by creating triangles out of quadrilaterals. The load bearing deck is supported by horizontal cross-beams attached to the bottom of the radials, close to the junction of two tangents, where the applied load can balance the resultant of the two compressive forces from the tangents.
History of the design
Etheridge had previously been foreman to James King (d. 1744), master carpenter during the building of the first Westminster Bridge 1737–50. Of King it was reported that:
Mr K. was, without education, a man of ingenuity and considerable self-taught mechanical knowledge.
[Gentleman’s Magazine, Vol. 65, Pt 2, July 1795, p. 618]
 It is to James King that the system of tangent-and-radial trussing may be attributed: he used it in his 1737 design for a timber Westminster Bridge (seen right):
It is to James King that the system of tangent-and-radial trussing may be attributed: he used it in his 1737 design for a timber Westminster Bridge (seen right):
a curious wooden Superstructure, of the Invention and Design of … Mr. James King. … the Model of this Superstructure was … shown and explained to a great many Persons of the first Rank in the Kingdom, and to many others, and generally approved of, as the most curious of its Kind…
[A Description of Westminster Bridge, by Charles Labelye, 1751, p. 7]
This is the earliest known example of this style of tangent-and-radial truss design, but it was not proceeded with after some preparatory structures were damaged when the Thames froze over in the winter of 1739–40. [Arch bridges and their builders 1735–1835, by Ted Ruddock, p. 10]
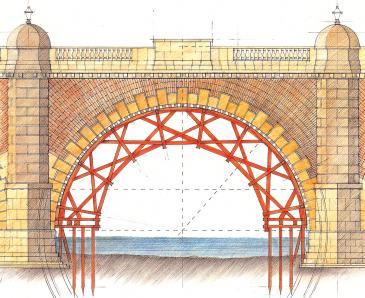 In 1741, construction of a Westminster Bridge in stone commenced, and James King was appointed again to erect the wooden centres on which the stone arches would be laid. He used the same system of tangent-and-radial trussing for his wooden arched centres as he had employed in his earlier design for a wooden bridge. This design permitted shipping to pass under the arches while they were being erected.
In 1741, construction of a Westminster Bridge in stone commenced, and James King was appointed again to erect the wooden centres on which the stone arches would be laid. He used the same system of tangent-and-radial trussing for his wooden arched centres as he had employed in his earlier design for a wooden bridge. This design permitted shipping to pass under the arches while they were being erected.
Etheridge took over the work at Westminster after King’s death in 1744.
 Paintings by Canaletto show Westminster Bridge under construction with centres of this design under each arch. In the detail of 1746 shown right, wooden centres can be seen still in position under the arches, and scaffolding around some of the piers. The balustrade above the arches is not yet built.
Paintings by Canaletto show Westminster Bridge under construction with centres of this design under each arch. In the detail of 1746 shown right, wooden centres can be seen still in position under the arches, and scaffolding around some of the piers. The balustrade above the arches is not yet built.
Source: Detail from: The River Thames looking towards Westminster from Lambeth, by Canaletto, The Lobkowicz Collections, Prague.
 Another painting by Canaletto, 1747, purports to show a view of London through an arch of Westminster Bridge while the wooden centre was still in place. St Paul’s can be seen on the right. But the artist has fallen into serious error: he has shown the wooden arch to have a semi-circular outline, when we know it was made from intersecting tangents. Also, the perspective of the buildings seems to have been taken from roof-level rather than water-level. So I suspect that Canaletto invented most of this picture.
Another painting by Canaletto, 1747, purports to show a view of London through an arch of Westminster Bridge while the wooden centre was still in place. St Paul’s can be seen on the right. But the artist has fallen into serious error: he has shown the wooden arch to have a semi-circular outline, when we know it was made from intersecting tangents. Also, the perspective of the buildings seems to have been taken from roof-level rather than water-level. So I suspect that Canaletto invented most of this picture.
Source: London: Seen Through an Arch of Westminster Bridge, private collection.
Etheridge went on to use this system of trussing again in his designs for Walton and Queens’, in 1748/9. In the 18th century, a generic description for designs of this sort was geometrical construction, from which one might speculate that the phrase Mathematical Bridge could be derived. [Arch bridges and their builders 1735–1835, by Ted Ruddock, p. 35]
Other bridges to similar designs
Old Walton Bridge
 The old Walton Bridge was also designed by William Etheridge, built by a Mr White of Weybridge during 1748–50, and paid for by Samuel Dicker, later M.P. for Plymouth. This print of the Walton Bridge was published in the Gentleman’s Magazine of 1750, Supplement, pp. 588–9.
The old Walton Bridge was also designed by William Etheridge, built by a Mr White of Weybridge during 1748–50, and paid for by Samuel Dicker, later M.P. for Plymouth. This print of the Walton Bridge was published in the Gentleman’s Magazine of 1750, Supplement, pp. 588–9.
The Walton Bridge was much admired for its strength, contrivance and remarkably great arch
[Gentleman’s Magazine, Vol. 20, Nov 1750, p. 488], and was even described as the most beautiful wooden arch in the world
. [Descriptions to the plates of Thames Scenery, engraved by W.B. Cooke & G. Cooke, published by John Murray, 1818]
 It attracted Canaletto to paint it twice: this is a detail from the first, painted in 1754. The artist in the bottom left-hand corner is reputed to be Canaletto’s depiction of himself.
It attracted Canaletto to paint it twice: this is a detail from the first, painted in 1754. The artist in the bottom left-hand corner is reputed to be Canaletto’s depiction of himself.
Source: A View of Walton Bridge, at Dulwich Picture Gallery.
 This is a detail from the second Canaletto, of 1755. The Walton Bridge’s main span was 130 feet, with two side arches of 44 feet. Unfortunately, it decayed and lasted only until 1783.
This is a detail from the second Canaletto, of 1755. The Walton Bridge’s main span was 130 feet, with two side arches of 44 feet. Unfortunately, it decayed and lasted only until 1783.
Source: Old Walton Bridge, at Yale Center for British Art.
One of the asserted merits of this design was described as:
The happy construction of this bridge was such, that being composed of timbers, tangent to a circle of a hundred feet in diameter, either of which falling into decay, might, with ease, be unscrewed; and, with equal facility, receive a new substitute, without disturbing the adjoining timbers.
[Picturesque views on the River Thames, by Samuel Ireland, 1792, Vol. 2, pp. 73-4]
Presumably, this process relied upon the triangulation in the trusses having sufficient redundancy that one timber could be removed while others took up the strain. No report is known of such a surgical repair ever having been carried out on either the Walton or the Queens’ bridge, but it is plausible that Etheridge’s model of the bridge for Queens’ was designed to demonstrate that possibility, with the screw-eyes offering an easy way for the joints to be unfastened, and individual timbers removed, to test the theory. Ironically, the failure of the Walton Bridge, and the problems afflicting the pre-1866 bridge at Queens’, were caused by decay of the horizontal cross-beams between the trusses, and not to any failure of the tangent-and-radial trusses themselves that might have been repairable in this way.
Garret Hostel Lane bridge, Cambridge
 There once was a bridge of similar design on the River Cam at the site of the present Garret Hostel Bridge, between Trinity Hall and Trinity College, built in 1769. In 1812:
There once was a bridge of similar design on the River Cam at the site of the present Garret Hostel Bridge, between Trinity Hall and Trinity College, built in 1769. In 1812: On the 2nd of July, Garret Hostel bridge broke down. It had been in a decayed state for a considerable time, and the passage over it had been stopped for several days previously. It was frequently called the mathematical bridge, and was erected in 1769, from a design by Mr. Essex.
[Annals of Cambridge, C.H. Cooper, vol. IV, p. 503]. That was the same Mr Essex who had built the bridge at Queens’ in 1749.
This view was engraved by Richard Hopkins Leach (1794–1851), from a drawing by his son Barnett Leach (1823–1880, 5th of that name). It was published in 1921 as the frontispiece of Cambridge Revisited, by Arthur Beales Gray (1867–1938), when the title and date were added. The view is dated Circa 1810
, but the print must have been drawn and engraved later (perhaps from an earlier painting), maybe in the 1840s when other views from this couple are known.
Iffley Lock, Oxford
 The footbridge at Iffley Lock, Oxford, is a scaled-down and simplified copy of the Queens’ bridge, built 1924 in teak, by the Thames Conservancy, to the design of their Chief Engineer, Griffith John Griffiths (1873–1940), M.I.C.E. [The Newton Bridge at Iffley, by G.J. Griffiths, in The Dial, No. 50, 1925 Lent, pp. 24–5]
The footbridge at Iffley Lock, Oxford, is a scaled-down and simplified copy of the Queens’ bridge, built 1924 in teak, by the Thames Conservancy, to the design of their Chief Engineer, Griffith John Griffiths (1873–1940), M.I.C.E. [The Newton Bridge at Iffley, by G.J. Griffiths, in The Dial, No. 50, 1925 Lent, pp. 24–5]
The simplified design does not reproduce all the original features of the joinery of the Queens’ bridge. At Queens’ the tangents are broken into multiple short lengths with lap splice joints: at Iffley each tangent consists of only two lengths of wood simply bolted together side-by-side at the central arch: this change means that the Iffley bridge does not satisfy the 18th century design intention that individual timbers could be replaced without dismantling the bridge. The radials are split into separated halves, whereas, at Queens’, the halves of the radials are butted together, with the tangent joints mortised into them. The cross-beams (carrying the load of the footway) under the arch, at Queens’ are connected to the radials with external iron straps, whereas, at Iffley, they are bolted from underneath to hidden steel plates through which the bottom bolt of each radial passes.
Winchester
 There was a footbridge at Winchester to a similar design which lasted until 1976 [Ruddock, p. 35]. This was on the Itchen Navigation at location 51° 03′ 13.7″N, 01° 18′ 33.2″W [OS maps 1930s–60s]. It was built by Winchester College in 1928 to provide a route to their Palmer Field across the water meadows. The Warden of New College Oxford suggested that the Iffley design be considered [WinColl archives A4/1/26, Estates & Finance Ctte minutes, 1927 Oct 1]. The drawings of the Iffley bridge were obtained from the Thames Conservancy, and it was agreed to seek estimates for a similar bridge in oak [WinColl archives A1/10, GB Minutes, 1927 Nov 5]. An estimate was accepted [ibid. 1928 Feb], and construction was reported as complete [ibid. 1928 Nov]. [This photo by Peter Oates 1976]
There was a footbridge at Winchester to a similar design which lasted until 1976 [Ruddock, p. 35]. This was on the Itchen Navigation at location 51° 03′ 13.7″N, 01° 18′ 33.2″W [OS maps 1930s–60s]. It was built by Winchester College in 1928 to provide a route to their Palmer Field across the water meadows. The Warden of New College Oxford suggested that the Iffley design be considered [WinColl archives A4/1/26, Estates & Finance Ctte minutes, 1927 Oct 1]. The drawings of the Iffley bridge were obtained from the Thames Conservancy, and it was agreed to seek estimates for a similar bridge in oak [WinColl archives A1/10, GB Minutes, 1927 Nov 5]. An estimate was accepted [ibid. 1928 Feb], and construction was reported as complete [ibid. 1928 Nov]. [This photo by Peter Oates 1976]
 In the bridge as built, although the overall design resembles the Iffley bridge, there are differences of detail.
In the bridge as built, although the overall design resembles the Iffley bridge, there are differences of detail.
In this photograph [WinColl archives M37/15, ca 1970s], there is cracking evident at the bottom of some of the radials: might this be because the cross-beams (bearing the load of the footway) had been screwed from underneath into the bottom end of the radials, end-on to the grain?
The Winchester bridge was dismantled in 1976. The abutments remain.
The myths and falsehoods concerning the Queens’ bridge
For a bridge whose history is so well-documented, it is curious that so many false stories have become associated with it. One’s curiosity is aroused as to how these stories originated. But there are difficulties in researching the origin of falsehoods: (a) with true history, there is always the prospect of discovering primary material which validates the fact, whereas with false stories, there will never be any primary material to discover; (b) it is easier to validate a true statement than it is to disprove a false statement; and (c) authors of printed works sometimes check their facts, and if a popular oral tradition does not pass that test, they pass over it without comment, rather than wasting time and space to state it and then refute it: so there can be a long delay between a myth gaining widespread dissemination and it first appearing in print. Nevertheless, I have tried to pull together some notes on the various myths, and the timings of their first appearances in printed material.
The name of the bridge:
There is no such thing as an “official name” for the bridge. It has never been named. Late 18th century minutes of the college refer to it as “Essex’s Bridge” or “The Essex Bridge”, after its builder, just as we still today refer to the “Essex Building”. [In that period, there was a need for some disambiguation of bridge references, as the college then had four bridges in all, so “Essex” would have served for that purpose.]
As noted above, the term “Mathematical Bridge” began to appear in guide-books from 1803 onwards: but the same term was being used in the same period also to refer to the similar bridge at Garret Hostel Lane, so the phrase might refer to the general style of design rather than to a specific bridge, or there might have been some transference of names between the two bridges.
The term “Newton’s Bridge” appears to have arrived later, and presumably derives from the myth that Newton designed the bridge. There is a passing reference to “Newton’s Bridge” in an account of a visitor from the USA in 1857, by which time the phrase must have been in colloquial use (in Trinity College, at least):
… today, a young scholar of Trinity … pointed out the rooms occupied by Newton, and showed us ‘Newton’s Bridge’ …
[Maria Mitchell : Life, Letters, and Journals, by Phebe Mitchell Kendall, 1896, p. 120]
The following first appeared in “The Cambridge Review” [Vol. 1, No. 23, 1880 May 22, p. 101]:
You should style Queens’ as “quaint,” then walk through it, and out over Newton’s Bridge — anecdote here — then continue through the backs to King’s Bridge.
[Egoistical Essays, in Cambridge Trifles; or, Splutterings from an Undergraduate Pen, by George Nugent-Bankes, 1881, p. 70]
Another visitor from the USA in 1896 recorded:
One afternoon I was strolling alone through the quadrangle of Queens’ College, without the aid of a cicerone, or even of a guidebook. Thinking I had seen all there was worth seeing on the premises, I was about to leave, when I met a bright-looking working lad who had come to the Cambridge summer meeting from Bolton on a prize scholarship. Having already seen him elsewhere, I asked him in a somewhat patronizing tone what he had found of interest in Queens’ College. He replied by asking me if I had seen the lodgings of Erasmus. “No,” I said. “Where are they?” The intelligent youth from the mills of Bolton then guided an American college graduate, a whilom lecturer on the Italian Renaissance, to a shrine more genuine than Sir Isaac Newton’s bridge or Milton’s mulberry tree or Shakespeare’s doubtful birthplace.
[Summer Schools in England, Scotland, France and Switzerland, by Herbert B. Adams, Ph.D., in Report of the Commissioner of Education for the year 1897–98, Vol. 1, p. 103]
The earliest instance of the name “Newton’s Bridge” in a printed guide-book or history of Cambridge that I have so far noted is from 1905:
The present Dial and the Bridge are commonly associated with the name of Sir Isaac Newton. “Newton’s Clock,” “Newton’s Bridge,” “Erasmus’ Walk,” “Milton’s Mulberry Tree” — the popular association of the great names has so much poetic glamour about it that one would wish to believe in each case the authenticity of the attribution. But the historic conscience and Cambridge accuracy alike compel the statement, as to clock and bridge, that Newton died in 1728, and the clock and dial are very precisely dated by Cole as being constructed in 1733, and the bridge as precisely by Dr Plumptre as built by Essex and designed by Etheridge in 1749.
[The Story of Cambridge, by Charles William Stubbs, 1905, p. 179]
The reference to Cole and the dates given by Stubbs were probably taken from Willis & Clark, 1886. We have better dates for the dial now.
The falsehood that Newton designed the bridge:
This popular myth goes hand-in-hand with using the name “Newton’s Bridge”. It is easily refuted by comparison of the relevant dates: Newton died in 1727; the bridge was built in 1749, and there is no record of Newton being involved at any stage, either before or after his death. As for the myth’s origin, little is known. One might speculate that, given the history of the design being known as a “Mathematical Bridge”, and this being Cambridge, then sooner or later Newton’s name would get dragged into it. Or maybe there was some transference from the mis-attribution of the Queens’ sundial to Newton: that mis-attribution had been started in 1753 by Carter, and had been continuously in print until refuted by Willis & Clark in 1886.
The earliest that I have found this myth in print was written in 1897:
The bridge itself dates from 1746, and is said to have been designed by Newton on a geometrical principle.
[Cambridge and its Colleges, by Alexander Hamilton Thompson, 1898 & 2nd ed. 1905, p. 124]
This mis-statement combines Carter’s incorrect date of 1746 with the misattribution to Newton: it was corrected in the third (1910) and later editions, so presumably the author had realised the errors.
The falsehood that the bridge was first built without fastenings at the joints:
How could such an absurd proposition ever gain popular acceptance? Without fastenings at the joints, the side trusses of the bridge might be liable to distort sideways, or spring apart. We have a photographic record dating back to the 1850s showing fastenings at the joints. The 1824 print drawn by Burford shows fastenings at the joints. Etheridge’s design model of 1748 has fastenings at the joints. Whether the fastenings were dowels, screws, or bolts-and-nuts, and whether they were visible or not, the structure would have needed fastenings at the joints, and must in fact have had them from the very beginning.
The myth of the bridge having been built without nails
appears to have achieved popular dissemination quite early in its history:
Proceeding onwards through an archway, you get to a bridge over the Cam, of very singular construction. It consists of a single arch of woodwork, and so framed that, without a single nail to bind the pieces together, it is firmly supported. It could be taken to pieces and put up again, in a very short time, and at a trifling expense. If I mistake not, this curiosity was erected at the instance, and under the direction, of the famous Dean Milner, then President of the college.
[Alma Mater, or, Seven Years at the University of Cambridge, by John Martin Frederick Wright, 1827, Vol. 1, p. 101]
In fact, the bridge was erected long before Milner arrived as a student at Queens’, so the factual reliability of this volume of reminiscences is placed in doubt. The report of the myth can be acccepted as a written note of what was then circulating as an oral tradition. Although published in 1827, the volume relates events from the period 1815 onwards. [This account of the bridge, although written by an ex-student of Trinity College, makes no reference to Newton, which might indicate that the Newton myth originated later than this period].
The falsehood that the bridge could not be rebuilt without introducing fastenings at the joints:
This myth was not seen in print from the 18th or 19th centuries: it appeared in 1910:
First we find ourselves with the old red brick fabric of Queens’ College on the one bank and the thicket of “Queens’ Grove” on the other, joined together by a wooden bridge, attributed to Sir Isaac Newton, the Great Natural Philosopher and discoverer of the Law of Gravity. A miracle of ingenious construction is this bridge, formed of a series of mutually supporting beams requiring not a single bolt to hold them together. Such at least it was till a few years ago, when the old timbers, after two hundred years’ wear, fell into decay and had to be replaced, as nearly in facsimile as modern skill could compass.
[Highways and Byways in Cambridge and Ely, by John William Edward Conybeare, 1910 reprinted 1923, p. 41]
Here we have most of the myths gathered together in print for the first time, I believe. The phase “a few years ago” probably refers to the rebuilding of the bridge in 1905. This paragraph survived unchanged in the reprint of 1923, and in the modern facsimile reprints. So it appears that the Revd Conybeare, former Vicar of Barrington and a Cambridge resident, might be the person most responsible for starting the dissemination of these myths. He had been a student of Trinity College (1862–66), and I surmise that he might have been exposed to many Newton legends there, including perhaps the myth of Newton having been the designer of the Queens’ bridge. Had Conybeare checked with Willis & Clark 1886, or Atkinson 1897, he would have discovered the true facts. Since he did not refer to any authorities for the identity of the designer, he probably did not do so for the “requiring not a single bolt” assertion either.
The myth that the bridge was originally built without fastenings at the joints, but could not be rebuilt successfully without introducing fastenings at the joints, might owe its origin to a change in the nature of the fastenings during the 1905 rebuilding. A study of photographs of the pre-1905 bridge shows that the fastenings were visible only on the outer elevations of the side trusses, and not on the inner elevations seen by those passing over the bridge. The fastenings of the post-1905 bridge are bolts-and-nuts which pass right through the joints and are visible on both sides. Perhaps, after the rebuilding, the sight of bolt-heads on the inner elevations, where there had been none before, led passers-by to imagine that the previous bridge had not required fastenings at the joints.
The falsehood that the designer of the bridge was a student or a Fellow:
The designer of the bridge is known to have been William Etheridge, the builder was James Essex: both lives are documented [see Further reading below], and neither attended any university. A Cambridge Alumni Database does not include any Etheridge or any Essex of the correct name and relevant period. This myth was seen in print in 1976:
The ‘Mathematical’ Bridge as we know it today was built in 1749–50 by James Essex, designed by W. Etheridge, an undergraduate.
[Cam bridges, by Richard J. Pierpoint, 1976, p. 6]
This falsehood, along with the next two related falsehoods, was reproduced in 1985:
This intriguing structure was designed in 1749 by an undergraduate, W. Etheridge, and constructed in 1749–50 by James Essex.
[Cambridge Architecture, by Tim Rawle, 1985, p. 185]
and the same falsehoods survived in the edition of 1993. In a combination of two myths, one sometimes hears the false story that the bridge was designed by “a student of Newton”.
The falsehood that the designer of the bridge had visited China:
The lives of William Etheridge and James Essex are documented [see Further reading below], and no visit to China is recorded in either case. This myth was seen in print in 1976:
The student Etheridge had just returned from a visit to China and perhaps the Mathematical Bridge may have been a copy of a Chinese Bridge.
[Cam bridges, by Richard J. Pierpoint, 1976, p. 7]
Again, this falsehood was reproduced in 1985 and 1993:
It is interesting to note that Etheridge had visited China while an undergraduate, as the bridge has a strong Oriental flavour to it.
[Cambridge Architecture, by Tim Rawle, 1985, p. 185]
The falsehood that the design of the bridge is of Chinese style, or a copy of a Chinese bridge:
Again, this myth was seen in print in 1976, 1985 & 1993 [see previous paragraph], and can also be seen in the photograph of the 1924 footbridge at Iffley Lock [above]. In the 18th century, many bridges in English parks and gardens were built to a design either in Palladian style, or in a style then called “Chinese”: both were popular and in high fashion. But the bridges designed by William Etheridge (the design inherited from James King) with tangent-and-radial trusses did not truly conform either to the Palladian or to the Chinese ideals. As far as is known, nowhere in the world are there examples of tangent-and-radial truss bridges, other than those derived from the Old Westminster Bridge of James King. It is probable that 18th century taste, attuned to Palladian and Chinese styles, would have accepted the tangent-and-radial truss style of bridges with enthusiasm, and this certainly seems to have been the case with the Walton bridge. But that is no case for describing the Queens’ Bridge as being of Chinese design or origin.
The falsehood that the design of the Mathematical Bridge is similar to a design by Leonardo da Vinci:
The myth of an association between the design of the Mathematical Bridge and the design of a self-supporting bridge by Leonardo da Vinci seems to have emerged around 2018 [Chaos Science], reinforced by an anonymous edit with no citations in 2019 of the Wikipedia page [wiki history] for the Mathematical Bridge. There are earlier web pages on the da Vinci design [2015][2017][2017], but none of them suggest a similarity with the Mathematical Bridge, until one viewer-added comment on the latter. In reality, the only similarities between the two designs are that they are (a) bridges; and (b) made of wood. Everything else is fundamentally different. The bridge design by James King uses the principle of a voussoir arch to keep the tangential timbers in compression, without bending moment: it requires strong abutments to balance the forces at the springing of the arch. By contrast, da Vinci’s design uses a series of levers and fulcrums, in which the tangential timbers appear to suffer considerable bending moments, and is self-standing, requiring no abutments. There could scarcely be any greater difference in bridge design principles. [As a side note, it is interesting to note that, in the da Vinci-inspired bridges built both at Stuttgart and at Freiburg, the design was modified so that the tangential timbers were butted end-to-end at the fulcrum points, enabling some compressive action to be transmitted along the arch: this must have improved their strength].
The falsehood that the bridge was rebuilt in 1902:
The date of 1902 (in error for 1905) is given in many respectable publications from the 1950s onwards, such as An Inventory of the Historical Monuments in the City of Cambridge, by the Royal Commission on Historical Monuments (England), and all publications that copy from it. The error is first seen in the caption to Plate 28 in Browne & Seltman, 1951, and all other instances of the false date of 1902 seem to derive from that one. There also appears to be no evidence in support of the claim in Browne & Seltman that the bridge was also rebuilt in 1895.
The falsehood that the builder of the bridge was John Michell (Fellow):
The bridge has also been mis-attributed to John Michell, appearing in print in 1871:
John Michell may perhaps be better known as the builder of the mathematical bridge across the Cam, at Queen’s College, Cambridge
[English Mechanic and World of Science, Vol. 13, No. 325, 1871 June 16, p. 310]
in a letter from the pseudonymous Khoda Bux
, later identified as Andrew Thomas Turton Peterson, great-grandson of Michell. The letter relied on oral tradition within the family, and some of its statements have been questioned by later scholars [for instance: Memoir of John Michell, by Sir Archibald Geikie, 1918, pp. 14–19; The Reverend John Michell: A Letter from his Great-grandson, by Eric Hutton, in The Antiquarian Astronomer, No. 3, 2006, pp. 65–8]. Michell was an undergraduate at Queens’ from 1742, and appointed a Fellow in 1749, the year after Etheridge’s model of the bridge had been paid for. He would certainly have witnessed the bridge being constructed, but he cannot be said to have been the “builder”, in a literal sense.
Speculation
How did Etheridge and Queens’ College become introduced to each other?
Etheridge had no known connection with Cambridge. At the time that the model for Queens’ was made, he was working as master carpenter at Westminster Bridge, with no particular recognition outside of London. No bridge to his design had ever been built. The bridge at Walton, which would provide a significant boost to his reputation, had yet to be built. What led the college to commission a model of a bridge design from someone who had never yet built a bridge?
Further reading:
1886: The Architectural History of the University of Cambridge, by Robert Willis and John Willis Clark, Vol. 2, pp. 55–6. (OCLC 6104300)
1886: ibid., Vol. 3, pp. 540–6. [account of James Essex]
1888: Journal of a tour through part of Flanders and France in August, 1773, by James Essex, F.S.A., ed. William Milner Fawcett, Cambridge Antiquarian Society Octavo Publications No. XXIV, pp. vii–xxxvi. (OCLC 3323186) [account of James Essex]
1889: Essex, James, by John Willis Clark, in Dictionary of National Biography, Vol. 18, pp. 5–7.
1925: The Newton Bridge at Iffley, by Griffith John Griffiths, in The Dial, No. 50, Lent Term 1925, pp. 24–5.
1951: A Pictorial History of the Queen’s College of Saint Margaret and Saint Bernard, commonly called Queens’ College Cambridge, 1448–1948, by Archibald Douglas Browne (1889–1977) & Charles Theodore Seltman, Plate 28. (OCLC 7790464)
1954: A Biographical Dictionary of English Architects 1660–1840, ed. Howard Montagu Colvin; (OCLC 2172754)
Essex, James at pp. 197–200, Etheridge, William at p. 200, King, James at p. 347;
1978: 2nd edition as A Biographical Dictionary of British Architects 1600–1840; (ISBN 978-0-7195-3328-0)
Essex, James at pp. 297–300, Etheridge, William at p. 300, King, James at pp. 494–5;
1995: 3rd edition; (ISBN 978-0-300-06091-1)
Essex, James at pp. 350–3, Etheridge, William at p. 353, King, James at p. 587;
2008: 4th edition; (ISBN 978-0-300-12508-5)
Essex, James at pp. 362–5, Etheridge, William at p. 365, King, James at pp. 619–20.
1979: Arch bridges and their builders 1735–1835, by Ted (Edward Campbell) Ruddock (1930–2015). (ISBN 978-0-521-21816-0)
1979: Old Westminster Bridge : the bridge of fools, by Richard John Boileau Walker. (ISBN 978-0-7153-7837-3)
1984: The Ingenious Mr Essex, Architect, by Thomas Hugh Cocke. (OCLC 85059986)
1987: A History of Queens’ College, Cambridge, 1448–1986, by John David Twigg, p. 311. (ISBN 978-0-85115-488-6)
1992: Queens’ Bridge, by Gunnar de Vries, in Industrial Design 02: Zwei Forschungsberichte, ed. Lambert Rosenbusch, pp. 6–18. (ISBN 978-3-931185-27-5)
2002: A Biographical Dictionary of Civil Engineers in Great Britain and Ireland 1500–1830, ed. Alec Westley Skempton; (ISBN 978-0-7277-2939-2)
Essex, James, by Peter Stanley Miles Cross-Rudkin at pp. 216–7;
Etheridge, William, by Peter Stanley Miles Cross-Rudkin at pp. 217–8.
2004: Essex, James (bap. 1722, d. 1784), by Thomas Hugh Cocke, in Oxford Dictionary of National Biography.